

Include "\ SrcALL \ 68000 _Macros.asm " Ram Variables Cursor_X equ $00FF0000 Ram for Cursor Xpos Cursor_Y equ $00FF0000 + 1 Ram for Cursor Ypos conwayTilemapRam equ $00FF1000 conwayBackupTilemapRam equ $00FF2000 Video Ports VDP_data EQU $C00000 VDP data, R/W word or longword access only VDP_ctrl EQU $C00004 VDP control, word or longword writes only constants ROWLENGTH equ 40 Traps DC.L $FFFFFE00 SP register value DC.L ProgramStart Start of Program Code DS.L 7, IntReturn bus err,addr err,illegal inst,divzero,CHK,TRAPV,priv viol DC.L IntReturn TRACE DC.L IntReturn Line A (1010) emulator DC.L IntReturn Line F (1111) emulator DS.L 4, IntReturn Reserverd /Coprocessor/Format err/ Uninit Interrupt DS.L 8, IntReturn Reserved DC.L IntReturn spurious interrupt DC.L IntReturn IRQ level 1 DC.L IntReturn IRQ level 2 EXT DC.L IntReturn IRQ level 3 DC.L IntReturn IRQ level 4 Hsync DC.L IntReturn IRQ level 5 DC.L IntReturn IRQ level 6 Vsync DC.L IntReturn IRQ level 7 DS.L 16, IntReturn TRAPs DS.L 16, IntReturn Misc (FP/MMU) Header DC.B " SEGA GENESIS " System Name DC.B " ( C ) CHBI " Copyright DC.B " 2019. This way, updates don't impact the outcome of the rest of the cells down the line (which would go against the rules of the game, as all cell births/deaths happen simultaneously.) Every iteration of the main loop does the same thing: check neighbors of each cell in the grid, write the next generation to a buffer, copy that buffer over the original, and display the output.Grid boundaries are handled by using the classic trick of padding all sides with a value that's not used in the "real" grid, and always counts as a dead cell.I'm using the Genesis's foreground tilemap to create the graphics.(It was tested in the Fusion emulator but it should work anywhere.) This is the source code for a Sega Genesis game that you can compile with VASM. As always, thanks to Keith of Chibiakumas for the cartridge header and hardware routines. I went a little further and created a 40x30 grid, but this implementation is accurate and does have a blinker in it. Langton's ant - another well known cellular automaton.John Conway Inventing Game of Life - Numberphile video.Its creator John Conway, explains the game of life.One interacts with the Game of Life by creating an initial configuration and observing how it evolves.Īlthough you should test your implementation on more complex examples such as the glider in a larger universe, show the action of the blinker (three adjoining cells in a row all alive), over three generations, in a 3 by 3 grid. The "game" is actually a zero-player game, meaning that its evolution is determined by its initial state, needing no input from human players. We calculate N - the sum of live cells in C's eight-location neighbourhood, then cell C is alive or dead in the next generation based on the following table:Īssume cells beyond the boundary are always dead.

It is the best-known example of a cellular automaton.Ī cell C is represented by a 1 when alive, or 0 when dead, in an m-by-m (or m× m) square array of cells.
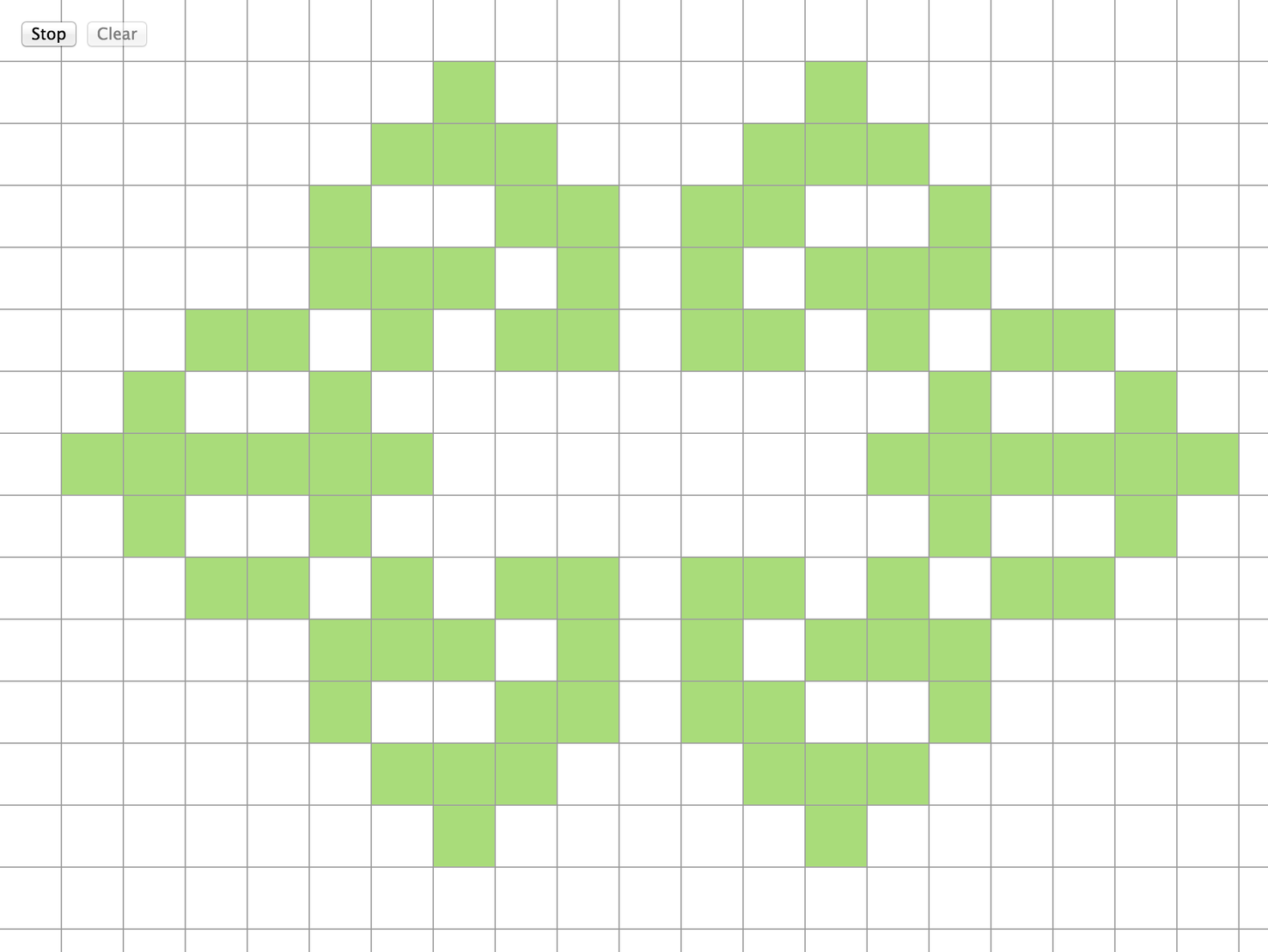

The Game of Life is a cellular automaton devised by the British mathematician John Horton Conway in 1970. You are encouraged to solve this task according to the task description, using any language you may know.


 0 kommentar(er)
0 kommentar(er)
